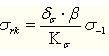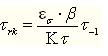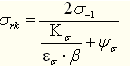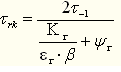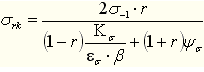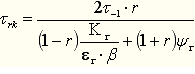2014年注评考试《机电设备评估基础》知识点:疲劳寿命理论及应用
为了帮助广大学员备战2014年注册资产评估师考试,正保会计网校精心为大家整理了注册资产评估师考试各科目知识点,希望能够提升您的备考效果,祝您学习愉快!
知识点:疲劳寿命理论及应用
一、基本概念
(一)应力
1.内力:物体的一部分对另一部分的机械作用。
2.应力:应力就是单位面积上的内力。
σ:正应力,法向应力,与截面垂直,正应力表示零件内部相邻两截面间拉伸和压缩的作用;
τ:切应力,剪应力,与截面平行,切应力表示相互错动的作用,正应力和切应力的向量和称为总应力。
正应力和切应力是度量零件强度的两个物理量,常用单位是兆帕(MPa)。
(二)应变
1.应变是外力作用引起的形状和尺寸的相对改变,是一个相对数。
2.当外力去掉以后,物体能完全恢复到原来的状态,那么这就叫做弹性应变;如果只能部分恢复到原来的状态,那么残留下来的那一部分变形称为塑性应变。
【提示】与正应力对应的是线应变,与切应力对应的是角应变。
(三)材料强度
图6-2所示为低碳钢试棒在受轴向静拉力时,轴向负荷P与绝对轴向变形Δl的关系曲线。
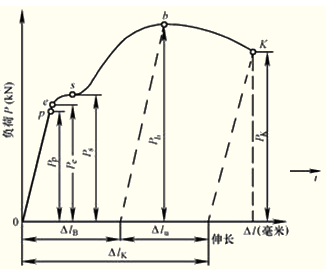
1.负荷较小时,材料的轴向变形与负荷成线性关系;负荷超过Pp后,呈非线性关系。保持线性关系的最大负荷为比例极限负荷Pp.与该点相对应的应力称为比例极限,用σp表示,也就是应力与应变为线性关系的最大应力。
2.负荷小于Pe时,材料的变形为弹性变形,大于Pe时则产生塑性变形,与该点相对应的应力为弹性极限σe.
3.当负荷增大到一定值时,在负荷不增加或减小的情况下,试样还继续伸长,这种现象叫屈服。屈服阶段的最小负荷是屈服点的负荷Ps,与之对应的应力称为屈服极限,用σs表示。
【提示】对没有出现明显屈服现象的材料,用产生0.2%残余变形的应力作为条件屈服极限。
4.当负荷达到一个最大值Pb,试样的某一截面开始急剧缩小,致使负荷下降,该负荷为强度极限负荷。与之相对应的应力称为强度极限或抗拉强度,用σb表示。它是材料拉断前的最大应力。
5.当负荷达到PK时,试样断裂。这个负荷称为断裂负荷。
【提示】屈服极限σs、强度极限σb是评价材料静强度的重要指标。
【小结】
|
比例极限 |
应力和应变、力和变形成线性关系的最大应力,用σp表示 |
|
弹性极限 |
保持弹性变形的最大应力,超过它就不再仅仅是弹性变形,还有塑性变形,用σe表示 |
|
屈服极限 |
开始出现屈服现象的应力,所谓屈服,就是负荷不再增加,但试件还在继续伸长的这种现象。屈服极限用σs表示 |
|
强度极限 |
材料拉断前的最大应力,也叫做抗拉强度,用σb表示 |
|
断裂负荷 |
试件断裂处的负荷 |
(四)许用应力
|
定义 |
许用应力是机械设计中,允许零件或构件承受的最大应力值。 |
|
公式 |
对于塑性材料(大多数结构钢、铝合金等): |
|
对于脆性材料(高强度钢、铸铁等): |
二、疲劳及疲劳寿命
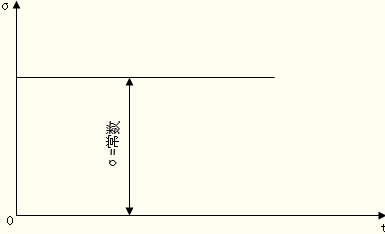
静应力:静应力就是应力的大小和方向不随时间而改变。
交变应力:它是指应力的大小和方向随时间呈周期性的变化的应力。
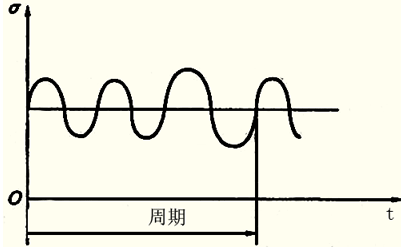
疲劳寿命:材料在疲劳破坏前所经历的应力循环次数称为疲劳寿命。
【提示】根据应力循环次数分为高周疲劳和低周疲劳,在机械工程中最常见的疲劳是高周疲劳。锅炉受到的是低周疲劳(第八章)
三、疲劳寿命曲线
1.零件的疲劳寿命与零件的应力水平有关,它们之间的关系可以用疲劳寿命曲线表示(S-N曲线)
(1)种类:应力-寿命曲线(σ-N曲线),应变-寿命曲线(δ-N曲线)。
(2)数学表达式:σmN=C (6-7)
式中:m、C——材料常数。
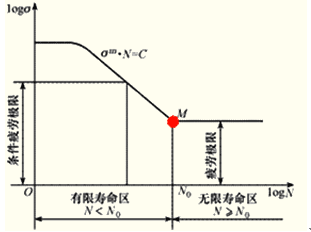
【小结1】水平起始点M对应的应力值σ叫做疲劳极限。①疲劳极限:是可以承受无限次应力循环而不会发生疲劳破坏的最大应力。②疲劳极限比材料静强度极限要低得多。
【小结2】对应M点的横坐标叫做循环基数,用符号N0来表示,N0一般是107,但是对于具体的材料、具体的循环特征,N0有所不同。
①在N0点右边的部分,是无限寿命区,如果承受的应力小于疲劳极限,试件就可以承受无限次应力循环而不发生疲劳破坏;
②N0点左边的区域为有限寿命区,又称为条件疲劳极限,即当材料所承受的最大应力大于它的疲劳极限时,只能承受有限次应力循环,而不能是无限次。
③N低于104~105时对应的有限寿命区称为低周疲劳区。
④在有限寿命区,应力和循环次数的关系用方程σmN=C来表示。
【提示】S-N曲线是由标准试件测试得出的,对于实际零件尺寸和表面状态与试件有差异,常存在由圆角、键槽等引起的应力集中,所以,在使用时必须引入应力集中系数K、尺寸系数ε、和表面系数β。
四、循环应力的特性
(1)交变应力的参数:最大应力σmax、最小应力σmin、平均应力、应力幅、循环特征。
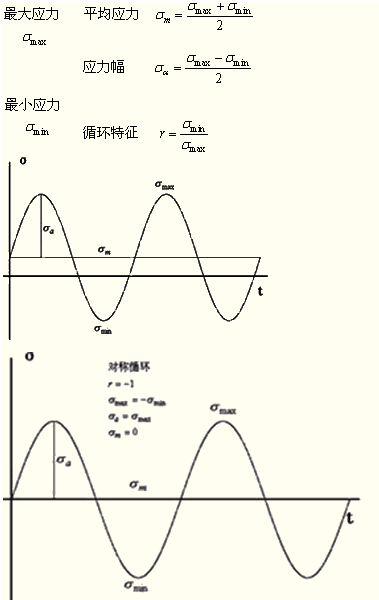
r=-1,称之为对称循环
|
循环应力 |
特点 |
|
对称循环应力 |
循环特征r等于-1;最大应力和最小应力大小相等,符号相反;平均应力等于0;应力幅等于最大应力。 |
|
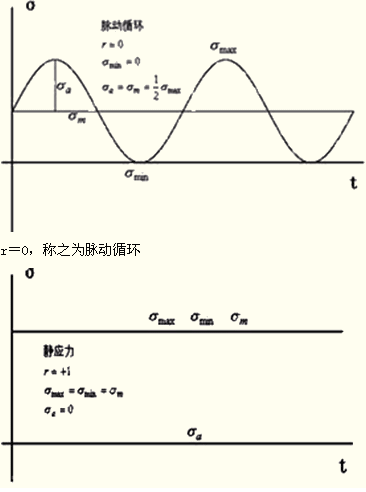
脉动循环应力 |
循环特征r等于0;应力幅等于平均应力,都等于二分之一最大应力;最小应力等于0。 |
|
静应力 |
循环特征r等于+1;最大应力等于最小应力,等于平均应力;应力幅等于0 。 |
【小结】疲劳极限的数值不仅和材料有关,还和循环特征有关,对称循环条件下,最容易发生疲劳破坏,相应的疲劳极限值最低,脉动循环好一点,所以,对一种材料的疲劳极限通常用σr表示,r这个下标代表循环特征,具体来说,对称循环时,材料的疲劳极限用σ-1表示,而脉动循环时,材料的疲劳极限用σ0表示,σ-1小于σ0.
(2)疲劳极限曲线
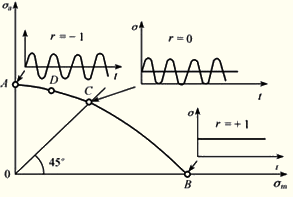
①A点表示对称循环条件下的疲劳极限;
②B点表示σα接近于0时的疲劳极限;
③C点表示脉动循环的疲劳极限。
【提示1】曲线上各点的疲劳寿命相等,这些曲线也称等寿命曲线。
【提示2】工程上,常将这条曲线简化为ACB折线,或者直接简化为AB直线,虽降低了计算精确度,但更趋于安全。
五、疲劳极限
考虑零件的应力循环特征、尺寸效应、表面状态应力集中等因素的零件疲劳极限如表6-1所示。
表6-1零件疲劳极限σrk 和τrk的计算公式
|
应力循环情况 |
弯曲或拉压时的σrk |
扭转时的τrk |
|
恒幅对称循环(r=-1) |
|
|
|
恒幅脉动循环(r=0) |
|
|
|
恒幅不对称循环 |
|
|
注:Kσ、Kτ为有效应力集中系数;εσ、ετ为尺寸系数;β为表面状态系数;ψσ、ψτ为不对称循环系数;r为最小应力σmax与最大应力σmin的比值。
|
有效应力集中系数K |
指在相同试验条件下,光滑试件与有应力集中的试件的疲劳极限之比(其确定方法有实验法和计算法两种)。 |
|
尺寸系数ε |
在相同情况下,尺寸为d的零件的疲劳极限与标准试件的疲劳极限之比。 |
|
表面状态系数β |
经过某种加工的零件的疲劳极限与标准试件的疲劳极限之比。表面粗糙度的值高于标准试件时β<1.0;用表面强化方法,如表面热处理和表面冷加工硬化等,可使β大于1.0。 |
|
不对称循环度系数Ψ |
指应力循环特征对疲劳极限的影响系数,Ψσ、Ψτ分别表示弯曲和扭转时的情况。 |
六、疲劳损伤积累理论
疲劳损伤积累理论认为,当零件所受的应力高于疲劳极限时,每一次应力循环都会对零件造成一定量的损伤,这种损伤是可以积累的;当损伤积累到临界值时,零件将发生疲劳破坏。
线性损伤积累理论认为,每一次循环载荷所产生的疲劳损伤是相互独立的,总损伤是每一次疲劳损伤的线性累加(帕姆格伦-迈因纳定理)。
损伤率达到100%时,发生疲劳损坏。
![]()
令N为以循环数表示的疲劳寿命,上式可以改写为:
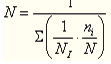
七、疲劳寿命理论的应用
机器设备主要失效形式是疲劳破坏。一般来讲,设备的结构寿命是决定整个设备自然使用寿命的基础,如起重机报废标准中规定:主梁报废即标志着安全使用寿命的终结,可申请整车报废。在机器设备评估中,疲劳寿命理论主要用于估算疲劳寿命和疲劳损伤。
1.对于重要设备的评估,我们必须根据设备所承受的实际载荷,使用疲劳寿命理论对设备的实际疲劳损伤程度和剩余寿命进行计算。其基本步骤如下:
(1)统计计算危险断面各种载荷所对应的名义应力σi及作用次数ni;
(2)根据S-N曲线确定每一载荷所对应的应力水平σi下,达到疲劳破坏的循环次数Ni;
(3)根据疲劳损伤积累理论计算每一应力水平σi下的损伤率ni/Ni;
(4)计算总损伤率 ![]() .
.
2.对于未进行疲劳寿命计算的机器设备,疲劳寿命理论可以用来估算这些设备的剩余物理寿命,其基本步骤如下:
(1)确定危险断面。有限寿命计算需要先知道应力值。计算时,首先分析承受载荷的情况,确定危险截面及其所承受应力的变化规律,并对这个截面进行疲劳寿命计算。如危险截面无法完全确定,则应对几个可能截面进行计算分析。
(2)确定应力。计算每一个载荷对应的应力值。
(3)计算应力循环次数。统计每一个载荷所对应的应力循环次数。
(4)确定各系数。考虑实际零件的形状、尺寸及表面状态,确定应力集中系数K、尺寸系数ε、表面系数β及不对称循环系数Ψ。
(5)计算修正后的应力。根据应力集中系数K、尺寸系数ε和表面系数β计算修正后零件的疲劳极限。
(6)计算疲劳损伤或疲劳寿命。查与σi对应的Ni,并计算疲劳损伤或疲劳寿命。