目录
01 概论
02 使用管理会计的基本方法,对现金流与产品的定价进行探讨
03 货币时间价值与销售情况探讨
04 货币时间价值与商品毁损的共同考虑
01 概论
·企业进行销售并回笼资金,是一个非常必要且重要的过程。
·如果企业的所有销售都是“现金销售”,那这个世界将会少很多麻烦。
·但事实是:不仅企业存在“赊销”的问题,同时也存在“质保”等方面的问题。
·因此本次课程将从三个阶段展开
·阶段1:使用管理会计的基本方法,主要涉及销售产品中的:
·现金流盈亏平衡点、整体定价策略以及扩展
·本阶段较为基础,难度一颗星
·阶段2:考虑了货币时间价值下的“平衡点”以及扩展
·本阶段同样较为基础,难度两颗星到三颗星
·阶段3:考虑了“损毁”情况和“货币时间价值”情况下的平衡点以及扩展
·本阶段的内容相对较难,难度四颗星到五颗星
02 使用管理会计的基本方法,对现金流与产品的定价进行探讨
现金流的盈亏平衡点
·说起现金流的盈亏平衡,也可以称为是“现金流回正”。
·即如果存在投资/产品销售的情况,现金流一般是“先流出,再流入”,也可以称为是“先有负向现金流,后有正向现金流”。
·现金流回正与否非常重要:
·回正时间越长、一般来说风险越高。
·回正可以充分衡量企业的流动性程度。
·基本结论:如果企业售卖产品(产品也是一种资产)的过程当中,产品非常畅销,则企业所面临的流动性风险较低。如果企业的产品销售虽然很赚钱,但销售周期很长,销售非常困难(如私人定制游艇、房地产等),则企业面临的流动性风险较高。
·那么,对现金流进行盈亏平衡的测算,会有如下一些定量计算方法
·方法1:传统法,也就是投资回收期payback period:
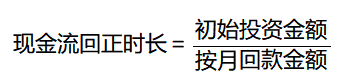
·举例:某企业投资1000元进行产品生产,每个月可以回款200元,则现金流回正时长为:
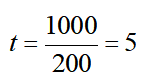
·方法2:在传统法上稍微进行改进,以应对回款金额非均衡的情况:
·举例:某企业投资1000元进行产品生产,每个月回款的金额为100、200、300、500和700,则其现金流回正时长为:
| 尚未回正金额(期初) |
按月回款金额 |
尚未回正金额(期末) |
| 1000 |
100 |
900 |
| 900 |
200 |
700 |
| 700 |
300 |
400 |
| 400 |
500 |
|
| |
700 |
|
| |
700 |
|
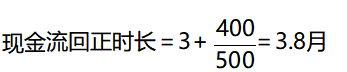
产品定价的盈亏平衡点
·说完了现金流的基本回正计算,我们再来说一下产品定价的盈亏平衡点。
·对于产品的盈亏平衡,基本上来说有两个大类
·情况1:已知产品的定价情况,计算盈亏平衡点
·情况2:无从得知产品的定价情况,必须要通过市场化的“试探”才能计算盈亏平衡点
·这种情况稍微有些复杂,涉及到概率方面的问题。我们来对这块进行着重探讨
·情况1:已知产品的定价情况
·已知定价情况,意味着所有东西对于企业来说都是“确定、可计量”的
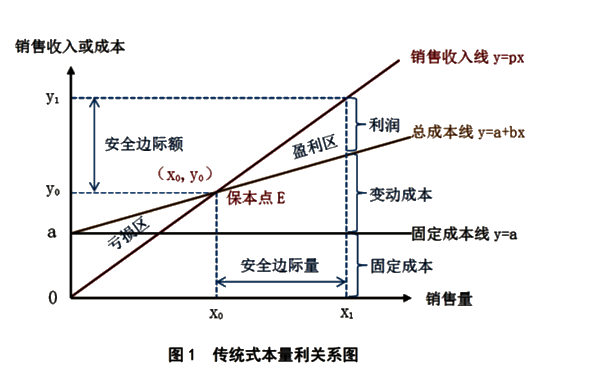
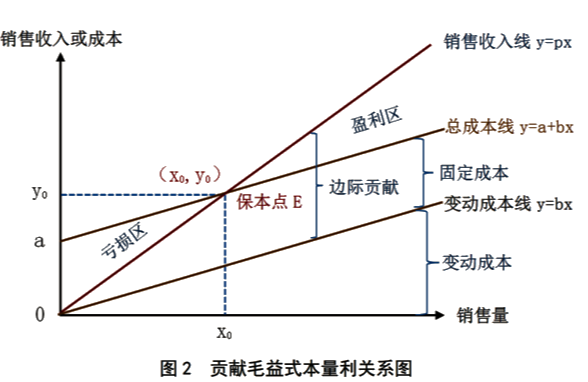
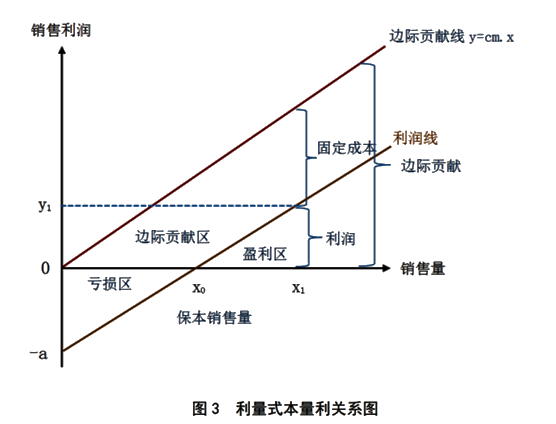
·因此,有如下计算公式:
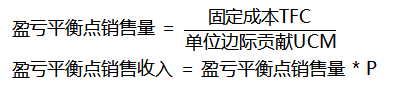
·举例:某企业有1000元的固定成本,其单位售价为10元,单位变动成本为8元。问其需要销售多少个产品,以及达到多少销售收入,才能达到盈亏平衡?
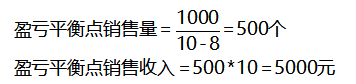
情况2:不知道企业的产品定价,或者就算一拍脑袋知道企业的产品定价,但无法确定市场是否能够接受这种定价。
在这种情况下,我们需要使用概率来进行确定。
为了方便理解,我们使用“航空公司”作为例子
·如果用航空公司的机票售卖作为例子,在正常市场定价情况下,到底机票定多少合适?
·首先放一张舱位表(以东航为例)
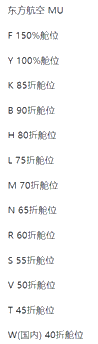
| 服务等级 |
舱位 |
消费积分
(标准里程*2%) |
升级积分
(标准里程*2%) |
升级次数 |
| 头等舱 |
F/P(国际、地区) |
200% |
200% |
2 |
| P(国内) |
125% |
125% |
1 |
| 公务舱 |
C/J/Z/O |
150% |
150% |
1.5 |
| W(国际、地区) |
125% |
125% |
1 |
| 经济舱 |
Y |
125% |
125% |
1 |
| K(国际、地区)B/E/H |
100% |
100% |
1 |
| L/M/N/R/S/V/T |
50% |
50% |
1 |
不能累积
的舱位 |
A/D/I/U/X/Q/K(国内)/W(国内)/G |
0 |
0 |
0 |
| 所有的包机航班不能享受里程累积 |
·作为航空公司,和各位所在企业一样,是不是想:我只要卖最贵的舱位就能最赚钱?
·答案正确!我只要卖最贵的舱位(F,Y),就好比各位所在企业的产品一样,定价到天上去,就可以实现最赚钱。
·但是有个问题:市场化情况下,真的有人买单吗?
·因此,航空公司只能退一步,当没人买票时(需求少)定价稍微低一些,当大家都买票时(需求高)定价稍微高一些,这是经济学常识,不过问题来了?
·如果我全部都定很低,结果东西一卖出来就被人一抢而空。老板后悔得肠子都青了,为什么不定高价!
·如果我全部都定得比较高,结果临近飞机起飞时都没坐满。飞机每飞一趟的固定成本是恒定的,没有坐满=丧失了挣钱的机会。
·各位想想你所在企业是不是一样的。假设你是个面包店,每天产能有限,面包保质期只有一天,过期作废。
·你到底是定稍微低价,还是定稍微高价?
·解决方法是什么?期望!
·正常情况的机票定价:以市场为调节,以概率为时机
·全称:Expected Marginal Seat Revenue EMSR法
·一般来说先卖最便宜的,如B、H等。如果一直买这种折扣机票,则航空公司最终会没有机会出卖Y舱,即收益无法最大化
·如果过早的介入出卖Y舱,即B/H这种折扣舱位放得过少,会有临近起飞都卖不出票的情况
·定价的核心逻辑:期望值最大
·什么叫期望值最大?
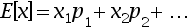
·回到前面的例子,假设航空公司有三个情况:起飞前10天,起飞前3天和起飞当天,以及各自的概率如下:
| 情况 |
预估可以卖出的票数 |
预估乘客可以接受的最高价格 |
该种情况下赚钱数 |
| 起飞前10天 |
100 |
800 |
80,000 |
| 起飞前3天 |
50 |
1,100 |
55,000 |
| 起飞当天 |
10 |
1,500 |
15,000 |
| |
|
|
150,000 |
·那么在这种情况下,起飞前10天我就多卖特价机票,起飞当天我就尽量卖头等舱和全价票
·回到各位企业的现实场景。如果各位卖面包,且面包不卖当天作废,你应该怎么办?
·是不是也借鉴之前的定价原则,以期望为定价基准来实现企业利益最大化?
| 情况 |
预估可以卖出的面包数 |
预估顾客可以接受的最高价格 |
该种情况下的赚钱数 |
| 早高峰 |
100 |
10 |
1,000 |
| 中午及下午 |
50 |
8 |
400 |
| 傍晚 |
80 |
6 |
480 |
| 深夜关门前 |
10 |
2 |
20 |
| |
|
|
1,900 |
·进一步,毕竟顾客不是机器人,有时候人家高兴了买一点,有时候不高兴就不买,是不是我们可以加上“概率”来进一步使得企业销售最大化判断更准确一些?
| 情况 |
预估可以卖出的面包数 |
预估这种情况的出现概率 |
预估顾客可以接受的最高价格 |
该种情况下的赚钱数 |
| 早高峰 |
100 |
95% |
10 |
950 |
| 中午及下午 |
50 |
90% |
8 |
360 |
| 傍晚 |
80 |
88% |
6 |
422 |
| 深夜关门前 |
10 |
70% |
2 |
14 |
| |
|
|
|
1,746 |
·再进一步,如果老板对销量非常不满意,说你们为什么这么无能,居然有存货?
·我们应该怎么办?很简单。降价
·但是,降价也是和前面一样,降价太多会亏,不降价会卖不完。怎么办?
·这时候就要用到人生中的法宝:试错法
·首先,作出如下降价,能发现什么问题吗?
| 情况 |
预估可以卖出的面包数 |
预估这种情况的出现概率 |
预估顾客可以接受的最高价格 |
该种情况下的赚钱数 |
| 早高峰 |
100 |
100% |
9.50 |
950 |
| 中午及下午 |
50 |
98% |
7.50 |
368 |
| 傍晚 |
80 |
90% |
5.00 |
360 |
| 深夜关门前 |
10 |
100% |
0.50 |
5 |
| |
|
|
|
1,683 |
·发现了问题,就把它往回调一点(具体反复调整过程忽略,假设最后我们得到的最优解如下)
| 情况 |
预估可以卖出的面包数 |
预估这种情况
的出现概率 |
预估顾客可以
接受的最高价格 |
该种情况下
的赚钱数 |
| 早高峰 |
100 |
100% |
9.80 |
980 |
| 中午及下午 |
50 |
98% |
7.90 |
387 |
| 傍晚 |
80 |
90% |
5.80 |
418 |
| 深夜关门前 |
10 |
100% |
1.20 |
12 |
| |
|
|
|
1,797 |
·再进一步,我们可以把这种“试错”以更多理论的方式来进行呈现,这里我们简单介绍一个高阶模型:聚合模型aggregate model。
·为了使得模型简单好理解,我们还是举例说明
·假设贵公司是卖煎饼的,下列是煎饼的定价情况,以及顾客的购买情况
煎饼定价:2元/个
一天之内
共计销售个数N |
出现这种销售情况的概率* |
每个顾客消费金额X |
出现这种消费情况的概率** |
| 100 |
1/3 |
10 |
0.5 |
| 200 |
1/3 |
12 |
0.3 |
| 300 |
1/3 |
14 |
0.2 |
·*注1:假设顾客到访完全是独立且随机的
·**注2:假设你已经知道便宜的卖得多,贵的卖得少
·根据聚合模型,我们可以得到在上述情况下总收入的期望方差
|
|
期望
|
方差
|
|
N
|
E[N]=200
|
σ2[N]=6666.67
|
|
X
|
E[X]=11.4
|
σ2[X]=2.44
|
E[S]=E[N]*E[X]=200*11.4=2,280
σ
2 [N]=E[N] σ
2 [X]+σ
2 [N](E[X])
2=866,888.4332
·进一步,我们将煎饼定价到2.5元一个,一天下来同样会有顾客的消费情况。注意在煎饼比前面贵的情况下,煎饼售卖数量会下降,但顾客的消费支出会变多。
·此处我们用“定量”的方式来进行判断是否应该涨价(而不是用定性的方式泛泛而谈)
一天之内
共计销售个数N |
出现这种销售情况的概率* |
每个顾客消费金额X |
出现这种消费情况的概率** |
| 100 |
0.5 |
10 |
0.4 |
| 200 |
0.3 |
12 |
0.45 |
| 300 |
0.2 |
14 |
0.15 |
| |
期望 |
方差 |
| N |
E[N]=170 |
σ2[N]=6100 |
| X |
E[X]=11.5 |
σ2[X]=1.95 |
E[S]=E[N]*E[X]=170*11.5=1,955
σ
2[N]=E[N]σ
2[X]+σ
2[N](E[X])
2=807,056.5
所以,该涨价吗?
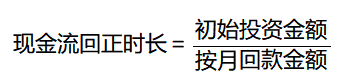
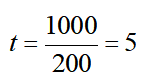
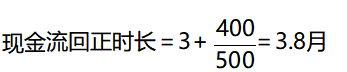



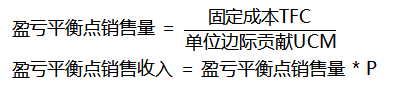
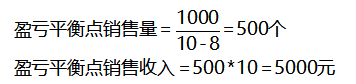
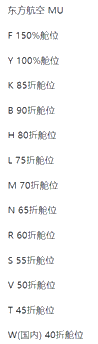
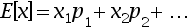
 添加学习顾问
添加学习顾问

