考情分析
本章是次重点章,主要介绍货币时间价值、收益与风险以及成本性态,是预算管理、筹资管理、投资管理、成本管理等后续章节的先导知识。本章题型比较全面,并可以单独(如收益与风险)或与其他章节的知识(如资本成本计算、项目投资管理、证券投资管理等)相结合考计算分析题或综合题,本章各年分值波动幅度较大,预计2024年分值在10分左右。
本章近三年题型、分值分布
| 年份 |
单选题 |
多选题 |
判断题 |
计算分析题 |
综合题 |
合计 |
| 2023-1 |
7.5 |
— |
1 |
5 |
— |
13.5 |
| 2022-1 |
4.5 |
— |
2 |
— |
4 |
10.5 |
| 2022-2 |
— |
— |
1 |
5 |
— |
6 |
| 2021-1 |
3 |
2 |
1 |
1 |
— |
7 |
| 2021-2 |
3 |
2 |
1 |
5 |
— |
11 |
| 2021-3 |
4.5 |
2 |
2 |
5 |
— |
13.5 |
主要考点
1.货币时间价值的计算
(1)复利终值和现值的计算
(2)年金终值和现值的计算
(3)利率的推算
①利用插值法推算利率
②名义利率与实际利率的换算
2.收益与风险
(1)资产收益的构成与类型
(2)资产的风险及其衡量
(3)风险管理
(4)证券资产组合的收益与风险
(5)资本资产定价模型
3.成本性态分析
(1)成本按性态分类:固定成本、变动成本、混合成本
(2)混合成本的分解方法
第一节 货币时间价值
知识点:货币时间价值的概念
1.货币时间价值的定义
在没有风险和没有通货膨胀情况下,货币在经过一定时间的投资和再投资后所增加的价值。
(1)货币进行投资会获取收益,进而产生价值增值。
(2)货币时间价值是投资收益率的基础。
①在没有风险也没有通货膨胀的情况下进行投资,所获得的收益即为货币时间价值。
用相对数表示的货币时间价值是指在没有风险和没有通货膨胀情况下资金市场的平均利率,称为纯粹利率或纯利率。
没有通货膨胀时,短期国债利率可以视为纯利率。
②在有风险和通货膨胀的情况下进行投资,投资者会要求获得更高的投资收益率作为补偿,即:
投资收益率=货币时间价值(即纯粹利率)+通货膨胀补贴+风险收益率(或风险补偿率)
2.货币时间价值观念
投资收益率的存在,使货币随着时间的推移产生价值增值,从而导致不同时点的单位货币具有不同的价值量。
(1)在其他条件相同的情况下,发生时间越早的单位货币,其价值量越大——今天的1块钱比明年的1块钱更值钱。
例如,在现金管理中,应加速回收应收账款,减缓支付应付账款。
(2)不同时点上的货币无法直接比较,必须“换算”为同一时点上的价值量(例如,0时点上的价值量即现值),才能比较和进行有关的财务决策。
例如,项目投资决策中,采用折现财务评价指标(如净现值等)进行财务可行性分析;证券价值评估中,债券或股票价值是其产生的未来现金流量的现值等。
3.货币时间价值计算
以投资收益率为依据,将某一时点上的货币价值量“换算” 为其他时点上的价值量,从而在不同时点的货币之间建立“经济上等效”的关联。
【示例】
在其他条件相同的情况下,今天收到100元和明年收到100元,哪个更好?
今天收到100元更好。
例如,将今天收到的100元存入银行,能够获得利息收益,明年可以得到100多元的本利和。
以一年期定期储蓄为例,在年利率为1.55%的条件下:
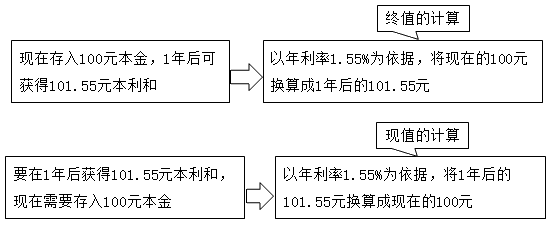
上述货币时间价值计算表明:在年利率为1.55%的条件下,现在的100元与1年后的101.55元在经济上等效。
知识点:货币时间价值计算的先导知识
1.时间轴

(1)以0为起点(目前进行价值评估及决策分析的时间点);
(2)0时点表示第1期的期初,自时点1开始,时间轴上的每一个点代表该期的期末及下期的期初。
2.终值与现值
| 终值(F) |
亦称将来值,是指现在一定量的货币按照某一收益率折算到未来某一时点所对应的金额,例如:本利和 |
| 现值(P) |
是指未来某一时点上一定量的货币按照某一收益率(折现率)折算到现在所对应的金额,例如:本金、内在价值 |
3.复利(利滚利)
每经过一个计息期,要将该期所派生的利息加入本金再计算利息,逐期滚动计算。
4.
复利终值和现值与
年金终值和现值的区别。
(1)
复利终值和现值:
一次性款项的终值和现值。
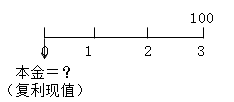
【示例】
现在存入100元,在第3年末的本利和为复利终值。

要在第3年末获得100元本利和,现在应存入的本金为复利现值。
(2)
年金终值和现值:定期、等额的系列收支款项的终值和现值的
合计数。
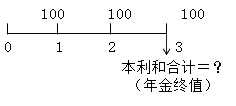
【示例】
从现在起的3年内,每年年末存入100元,则这3笔存款在第3年末的本利和合计数为年金终值。
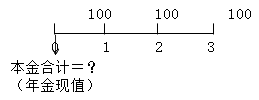
从现在起的3年内,每年末取出100元本利和,则这3笔存款在第1年初的本金合计数为年金现值。
复利终值和现值的计算
知识点:复利终值和现值的计算
——一次性款项的终值与现值的计算
1.复利终值(一次性款项的终值)

已知:①现值P(现在的一次性款项,例如本金),②计息期利率i(n期内每期复利1次的利率),③计息期数n(终值与现值之间的间隔期),求:终值F(例如本利和)。
【示例】
本金100元存入银行,年利率为10%,每年复利一次,则2年后的本利和(复利终值)为:

由此推出:F=P×(1+i)
n
=P×(F/P,i,n)
其中,(1+i)
n为复利终值系数,用符号表示为(F/P,i,n)。
【示例】
前例中2年后的本利和可计算如下:
F=100×(F/P,10%,2)=100×1.21=121(元)
【提示】
在货币时间价值计算中,利率i是指在
n期内每期复利一次的利率,即
“利率i”与
“期数n”应相互
匹配。
【示例】
如果利率i是
“每年复利一次”的
“年利率”,即以
“年”为计息期,则期数n就是
“年数”。
例如,年利率10%、1年复利1次(以“年”为计息期),则100元本金2年后的复利终值为:

如果利率i是
“每半年复利一次”的
“半年利率”,即以
“半年”为计息期,则期数n就是
“半年数”。
例如,年利率10%、1年复利2次,等效于半年利率5%、半年复利1次(以“半年”为计息期),则100元本金2年后的复利终值为:

2.复利现值(一次性款项的现值)——复利终值的逆运算

已知:①终值F(未来某一时点的一次性款项,例如本利和),②计息期利率i(n期内每期复利1次的利率),③计息期数n(终值与现值之间的间隔期),求:现值P(例如本金)。
由:F=P×(1+i)
n,可得:
P=F×(1+i)
-n=F×(P/F,i,n)
其中,(1+i)
-n为复利现值系数,用符号表示为(P/F,i,n)。
【示例】
已知银行存款的年利率为2%、每年复利一次,某投资者希望在第4年末获得10000元本利和,则现在应存入银行的本金为:
P=10000×(P/F,2%,4)=10000×0.9238=9238(元)
【提示】
复利终值和复利现值互为逆运算,复利终值系数(1+i)n与复利现值系数(1+i)-n互为倒数。
【例题·单项选择题】(2021年)
某工程项目现需投入3亿元,如延期一年,建设投入将增加10%。假设利率是5%,则延迟造成的投入现值增加额为( )亿元。
A.0.17
B.0.14
C.0.47
D.0.3
|
 |
 |
| |
『正确答案』B
『答案解析』延迟造成的投入现值的增加额=3×(1+10%)/(1+5%)-3=0.14(亿元)
|
【例题·判断题】(2023年)
期数不变的情况下,复利终值系数与利率呈反向变动关系。 ( )
|
 |
 |
| |
『正确答案』 ×
『答案解析』在期数(n)不变时,利率i越大,复利终值系数(1+i)n越大,即期数不变的情况下,复利终值系数与利率呈同向变动关系。
|















 添加学习顾问
添加学习顾问

