银行从业《风险管理》第一章第五节风险管理的数理基础四

　　正保会计网校为了帮助广大考生充分备考，整理了银行从业资格考试知识点供大家参考，希望对广大考生有所帮助，祝大家学习愉快，梦想成真！

第一章　风险管理基础

第五节　风险管理的数理基础

　　2.方差和标准差

　　资产收益率的不确定性就是风险的集中体现，而风险的大小可以由未来收益率与预期收益率的偏离程度来反映。假设资产的未来收益率有n种可能的取值r1， r2，…，rn，每种收益率对应出现的概率为pi，收益率r的第i个取值的偏离程度用[ri- E（R）]2 来计量，则资产的方差 Var（R）为

　　Var（R）=P1[r1-E（R）]2+ P2 [ r2-E（R）]2+…+Pn[rn-E（R）]2

　　方差的平方根称为标准差，用σ表示。在风险管理实践中，通常将标准差作为刻画风险的重要指标。资产收益率标准差越大，表明资产收益率的波动性越大。当标准差很小或接近于零时，资产的收益率基本稳定在预期收益水平，出现的不确定性程度逐渐减小。

　　3.正态分布

　　正态分布是描述连续型随机变量的一种重要概率分布（见图1-1）。若随机变量x的概率密度函数为

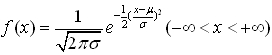
　　则称x服从参数为μ，σ的正态分布，记为N（μσ2），μ是正态分布的均值，σ2是方差。

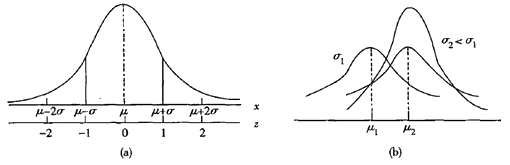
　　正态分布曲线具有如下重要性质：

　　（1）关于x=μ对称，在x=μ处曲线最高，在x=μ±σ处各有一个拐点；

　　（2）若固定σ，随μ值不同，曲线位置不同，故也称μ为位置参数；

　　（3）若固定μ，随σ值不同，曲线肥瘦不同，故也称σ为形状参数；

　　（4）整个曲线下面积为1；

　　（5）正态随机变量x落在距均值1倍、2倍、2.5倍标准差范围内的概率分别如下：

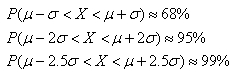
　　在商业银行的风险管理实践中，正态分布广泛应用于市场风险量化，经过修正后也可用于信用风险和操作风险量化。例如，可以用正态分布来描述交易类资产的收益率分布。一般来说，如果影响某一数量指标的随机因素非常多，而每个因素所起的作用相对有限，各个因素之间又近乎独立，则这个指标可以近似看做服从正态分布。

　　相关链接：银行从业资格考试《风险管理》知识点汇总
　　　　　　　 银行从业资格考试《风险管理》章节练习题汇总